Calcoli dell'induttore del condensatore

Gli induttori possono essere immaginati come l'opposto dei condensatori. La principale differenza tra un condensatore e un induttore è che un condensatore porta un dielettrico protettivo tra le sue piastre, che inibisce la conduzione della corrente attraverso i suoi terminali. Qui si comporta come un circuito aperto.

D'altra parte l'induttanza di un induttore è normalmente (sebbene non sempre) di resistenza incredibilmente bassa o minima. Si comporta essenzialmente come un circuito chiuso.

Dualità dell'induttore del condensatore

Esiste un termine unico in elettronica per questo tipo di relazione tra due parametri di un circuito o porzioni di un circuito. Gli elementi di questo tipo di coppia sono noti come duali l'uno dell'altro . Ad esempio, a seconda della capacità di condurre corrente, un circuito aperto è il doppio di un circuito chiuso.

In base allo stesso principio, un induttore è il doppio di un condensatore. La dualità di induttori e condensatori è molto più profonda della semplice capacità naturale di condurre corrente.

In questo articolo, confrontiamo il principio di funzionamento dell'induttore e del condensatore e valutiamo i risultati con calcoli e formule.

Nonostante il fatto che gli induttori normalmente si vedano raramente nei circuiti elettronici, dato che oggi sono per lo più sostituiti da amplificatori operazionali nei filtri attivi), le altre parti coinvolte in un circuito sembrano portare una certa quantità di induttanza.

L'autoinduttanza dei terminali di un condensatore o resistore diventa un grosso problema nei circuiti ad alta frequenza, il che spiega perché i resistori e i condensatori a montaggio superficiale senza piombo sono così frequentemente impiegati in tali applicazioni.

Equazioni di base del condensatore

L'equazione fondamentale per i condensatori è quella con cui è de fi nito il farad:

C = Q / I [Eq.19]

dove C è la capacità in farad, Q è la carica in coulomb e U è il pd tra le piastre in volt.

Attraverso l'Eq. 19, otteniamo una formula della forma Q = ∫ I dt + c dove c è la carica iniziale, se disponibile. Dopo aver identificato Q, siamo in grado di determinare U dall'Eq. 19:

U = 1 / C ∫ Io dt + c / C [Eq.21]

Una caratteristica importante di un condensatore può essere questa, se ad esso viene applicata una corrente periodica (di solito una corrente che oscilla sinusoidalmente), anche la carica sul condensatore e la tensione ai suoi capi fluttuano sinusoidalmente.

La curva di carica o tensione è una curva del coseno negativa, oppure possiamo immaginarla come una curva sinusoidale che è in ritardo rispetto alla curva di corrente di Pi / 2 operazioni (90 °).

L'equazione fondamentale che definisce henry, l'unità di induttanza, è

L = NΦ / I [Eq.22]

Con riferimento a una bobina singola, l'autoinduttanza in Henry può essere la relazione del flusso (il flusso magnetico<1) in weber multiplied by the number of winding N, (because the magnetic flux cuts through each turn), when a unit current passes through it (I = 1 A). An even more handy definition could be extracted from Eq. 22, using Neumann’s equation. This claims that:

U = N (dΦ / dt) [Eq.23]

Ciò che questa equazione suggerisce è il fatto che l'e.m.f. indotto all'interno di un induttore è relativo alla velocità di variazione del flusso collegata.

Quanto più velocemente varia il fl usso, tanto maggiore è l'e.m.f. Ad esempio, quando il flusso sull'induttore o sulla bobina aumenta alla velocità di 2 mWb s^-1e supponendo che la bobina abbia VENTICINQUE giri, allora U = 25x2 = 50V.

Il percorso della e.m.f. è tale da resistere alle variazioni di flusso come delineato dalla Legge di Lenz.

Questa verità è spesso evidenziata facendo precedere il lato destro dell'equazione con un segno meno, tuttavia fintanto che si crede che U sia il retro e.m.f., il segno potrebbe essere rimosso.

Differenziali

Il termine dΦ / dt nell'Eq. 23 indica ciò che abbiamo appreso come velocità di variazione del flusso. La frase è chiamata differenziale di Φ rispetto at, e un intero ramo dell'aritmetica è dedicato a lavorare con questo tipo di espressioni. La frase ha la forma di un singolo numero (dΦ) diviso per un'altra quantità (dt).

I differenziali vengono utilizzati per associare numerosi insiemi di proporzioni: dy / dx, ad esempio, mette in correlazione le variabili x e y. Quando un grafico viene tracciato utilizzando i valori di x sull'asse orizzontale e i valori di y sull'asse verticale, dy / dx indica quanto è ripida la pendenza, o gradiente, del grafico.

Se U è la tensione gate-source FET, dove T è la relativa corrente di drain, allora dI / dU indica la quantità con cui io cambia per determinati cambiamenti in U. In alternativa possiamo dire, dI / dU è la trans-conduttanza. Mentre si discute degli induttori, d d / dt potrebbe essere la velocità di variazione del flusso nel tempo.

Il calcolo di un differenziale può essere considerato come la procedura inversa di integrazione. Non c'è spazio sufficiente in questo articolo per esaminare la teoria della differenziazione, tuttavia definiremo una tabella delle grandezze comunemente usate insieme ai loro differenziali.

Differenziali standard

La tabella sopra funziona utilizzando I e t come fattori invece della routine x e y. In modo che i suoi dettagli siano specificamente pertinenti all'elettronica.

Ad esempio, considerando che I = 3t +2, il modo in cui I devia rispetto al tempo può essere visualizzato nel grafico di Fig. 38. Per trovare la velocità di variazione di I in qualsiasi momento, stimiamo dI / dt, da riferendosi alla tabella.

Il primo elemento nella funzione è 3t oppure, per formattarlo come prima riga della tabella, 3t¹. Se n = 1, il differenziale è 3t^1-1= 3t⁰.

Dal momento che t⁰= 1, il differenziale è 3.

La seconda quantità è 2, che può essere espressa come 2t⁰.

Questo cambia n = 0 e l'ampiezza del differenziale è zero. Il differenziale di una costante sarà sempre zero. Combinando entrambi questi elementi, abbiamo:

dI / dt = 3

In questa illustrazione il differenziale non include t, ciò significa che il differenziale non dipende dal tempo.

In parole povere, la pendenza o gradiente della curva in Fig. 38 è 3 continuamente tutto il tempo. La Figura 39 sotto mostra la curva per una funzione diversa, I = 4 sin 1.5t.

Con riferimento alla tabella, α = 1.5 eb = 0 in questa funzione. La tabella mostra, dl / dt = 4x1.5cos1.5t = 6cos 1.5t.

Questo ci informa sulla velocità di variazione istantanea di I. Ad esempio, at = 0,4, dI / dt = 6cos0,6 = 4,95. Questo si può notare nella Fig. 39, in cui la curva per 6 cos0.6t include il valore 4.95 quando t = 0.4.

Possiamo anche osservare che la pendenza della curva 4sin1.5t è 4,95 quando t = 0,4, come mostrato dalla tangente alla curva in quel punto, (rispetto alle diverse scale sui due assi).

Quando t = π / 3, un punto in cui la corrente è al suo massimo e costante, in questo caso dI / dt = 6cos (1.5xπ / 3): 0, corrispondente a zero cambiamento di corrente.

Al contrario, quando t = 2π / 3 e la corrente passa al livello più alto possibile da positivo a negativo, dI / dt = 6cosπ = -6, vediamo il suo valore negativo più alto, che mostra un'elevata riduzione di corrente.

Il semplice vantaggio dei differenziali è che ci consentono di determinare i tassi di variazione per funzioni molto più complesse rispetto a I = 4s in 1.5t, e senza dover tracciare le curve.

Torna ai calcoli

Riorganizzando i termini nell'Eq 22 otteniamo:

Φ = (L / N) I [Eq.24]

Dove L e N hanno dimensioni costanti, ma Φ e I possono avere valore rispetto al tempo.

Differenziando i due lati dell'equazione rispetto al tempo si ottiene:

dΦ / dt = (L / N) (dI / dt) [Eq. 25]

Unendo questa equazione con l'Eq.23 si ottiene:

U = N (L / N) (dI / dt) = L (dI / dt) [Eq.26]

Questo è un altro modo per esprimere il Henry . Possiamo dire che, una bobina avente autoinduttanza di 1 H, una variazione di corrente di 1 A s^-1genera un back e.m.f. di 1 V. Data una funzione che definisce come una corrente varia nel tempo, l'Eq. 26 ci aiuta a calcola il retro e.m.f. di un induttore in qualsiasi istante.

Di seguito sono riportati alcuni esempi.

A) I = 3 (una corrente costante di 3 A) dl / dt = 0. Non si trova nessuna variazione di corrente quindi il retro e.m.f. è zero.

B) I = 2t (corrente di rampa a) dI / dt = 2 A s^-1. Con una bobina che porta L = 0,25 H, la parte posteriore e.m.f. sarà costante a 0,25x2 = 0,5 V.

C) I = 4sin1.5t (la corrente sinusoidale data nell'illustrazione precedente dl / dt = 6cos 1.5t. Data una bobina con L = 0.1 H, la back emf istantanea è 0.6cos1.5t. La back emf segue la curva differenziale di Fig.39, ma con ampiezza 0,6 V invece di 6 A.

Capire i 'doppi'

Le due equazioni seguenti indicano rispettivamente l'equazione di un condensatore e di un induttore:

Ci aiuta a determinare il livello di tensione prodotto attraverso il componente dalla corrente che varia nel tempo secondo una funzione specifica.

Valutiamo il risultato ottenuto da differenziando i lati L e H dell'Eq.21 rispetto al tempo.

dU / dt = (1 / C) I

Come sappiamo la differenziazione è l'inverso dell'integrazione, la differenziazione di ∫I dt inverte l'integrazione, con solo I come risultato.

La differenziazione di c / C dà zero e la riorganizzazione dei termini produce quanto segue:

I = C.dU / dt [Eq.27]

Questo ci permette di conoscere la direzione della corrente sia che vada verso il condensatore sia che esca da esso, in risposta ad una tensione variabile in funzione di una data funzione.

La cosa interessante è che quanto sopra equazione della corrente del condensatore sembra simile all'equazione di tensione (26) di un induttore, che mostra il capacità, dualità di induttanza.

Allo stesso modo, la differenza di corrente e potenziale (pd) o il tasso di variazione di corrente e pd possono essere doppi quando applicati a condensatori e induttori.

Ora, integriamo l'equazione 26 rispetto al tempo per completare l'equazione quatret:

∫ U dt + c = LI

L'integrale di dI / dt è = I, riorganizziamo le espressioni per ottenere:

I = 1 / L∫ U dt + e / L

Anche questo sembra abbastanza simile all'Eq.21, dimostrando ulteriormente la duplice natura di capacità e induttanza, e il loro pd e corrente.

A questo punto abbiamo una serie di quattro equazioni che possono essere utilizzate per risolvere problemi relativi a condensatori e induttori.

Ad esempio, è possibile applicare l'Eq.27 per risolvere il problema come questo:

Problema: Un impulso di tensione applicato su un 100uF produce una curva come mostrato nella Fig sotto.

Questo può essere definito utilizzando la seguente funzione a tratti.

Calcola la corrente che si muove attraverso il condensatore e traccia i grafici corrispondenti.

Soluzione:

Per la prima fase applichiamo l'Eq.27

I = C (dU / dt) = 0

Per la seconda istanza in cui U potrebbe aumentare con un tasso costante:

I = C (dU / dt) = 3C = 300μA

Questo mostra una corrente di carica costante.

Per la terza fase in cui U scende in modo esponenziale:

Ciò indica che la corrente scorre via dal condensatore con una velocità decrescente esponenziale.

Relazione di fase

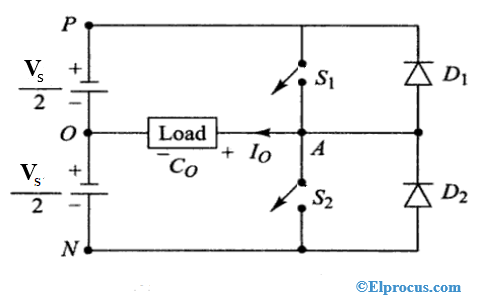
Nella figura abobe, un pd alternato è applicato a un induttore. Questo pd in qualsiasi istante può essere espresso come:

Dove Uo è il valore di picco del pd. Se analizziamo il circuito sotto forma di un loop e applichiamo la legge della tensione di Kirchhoff in senso orario, otteniamo:

Tuttavia, poiché la corrente qui è sinusoidale, i termini tra parentesi devono avere il valore uguale alla corrente di picco Io, quindi finalmente otteniamo:

Se confrontiamo l'Eq.29, e l'Eq.30, troviamo che la corrente I e la tensione U hanno la stessa frequenza, e io sono in ritardo rispetto a U di π / 2.

Le curve risultanti possono essere studiate nel diagramma seguente:

C

Questo mostra la relazione contrastante tra condensatore e induttore. Per una corrente di induttore la differenza di potenziale è in ritardo di π / 2, mentre per un condensatore, la corrente è superiore al pd. Ciò dimostra ancora una volta la duplice natura delle due componenti.